For some time I have been yearning to find a way to map relationships between sets of cards and words. My fascination arises from my love of words and numbers. Based on the concept of cryptomorphism, there must be one or more viable ways to formulate encodings that provide a means to derive meaning from patterns.
If you would like to jump to trying out the cipher, you can find it online here:
4-Letter Words from Cards (No information is sent away from your device.)
Here I propose one method specifically designed to map between sets of distinct 4-letter words and 4-card ordered ranks. This provides a way to derive a set of words for a 4-card spread, and map a 4-letter word to set of candidate cards. My tests so far have shown that overlap between distinct cards sets is well distributed and all combinations I have tried so far have matched at least one word.
Creating the Cipher
In order to make it more likely to generate words it is necessary to associate many letters with each card rank. Distributing the alphabet multiple times over 52 cards or only assigning one letter to a card would create too many combinations that will not match any word. There are other well-known attempts to associate cards with alphabets, such as Tarot's Major Arcana with Hebrew, but the trick is to discover methods that net a distinct subset of enough words and not so many it's noise.
The following table associates 5 letters with each card rank. Suits are not relevant to the selection of words, though they may be relevant to the associations of words to the meaning of the cards and nature of the elements for a 4-card set. Aside from generating the right balance of words, not too many or too few, the approach that I took is rooted in basic numerology. Letters have associations to ranks based on the alphabetic ordering as well as the numerological value of letters. For example, the letter A is 1, but so can be J since it is 10 and 1+0 = 1, and so can be S since it is 19 and 1+9 = 10. This allowed generation of almost 80% of the table as follows.
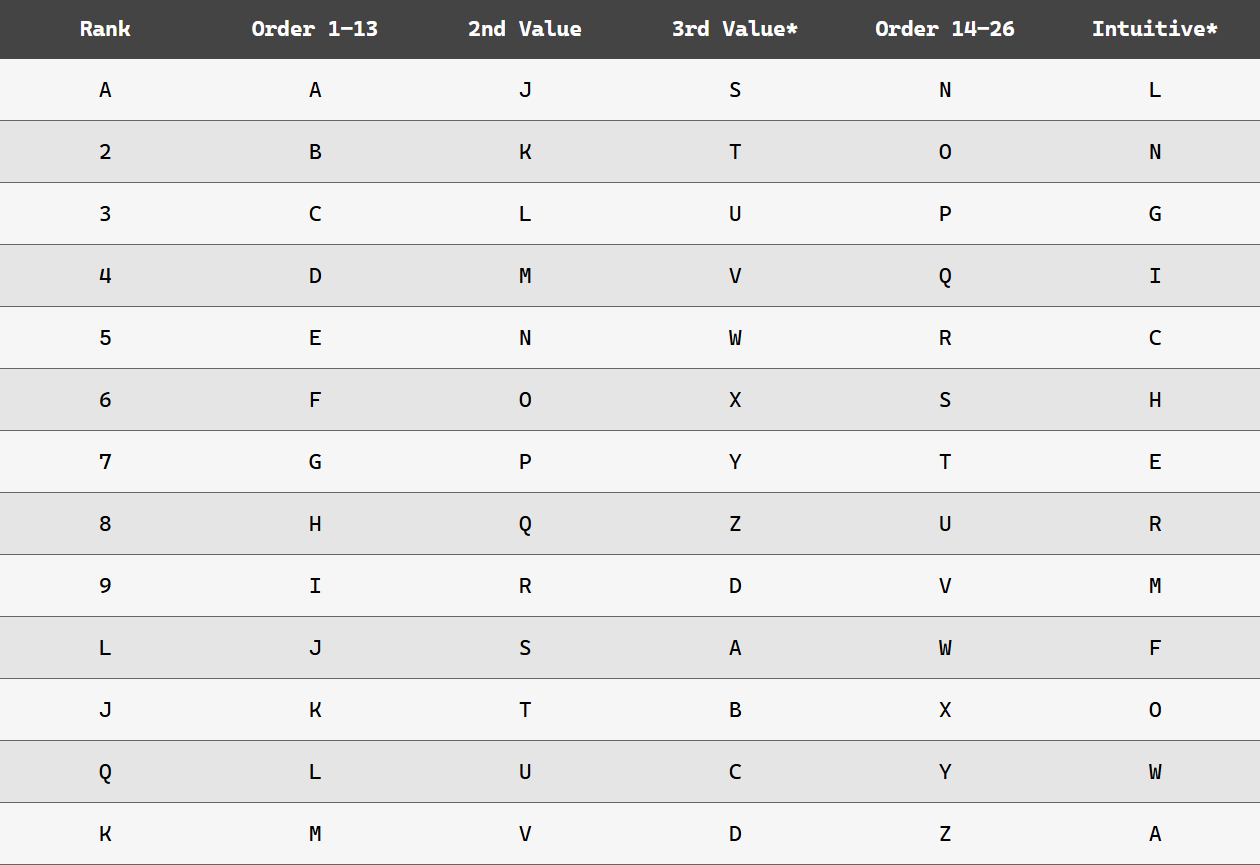
- Order 1-13: Letters in this column associate the letters at the positions in the alphabet 1 to 13 with the rank with the same numerical value Ace through King.
- 2nd Value: Letters in this column are the next letter in the alphabet based on the numerological value of the letter in the first column.
- 3rd Value: Letters in this column are the last letter in the alphabet based on the numerological value of the letter in the first column, except for 9=D and the 4 face card rows where we loop back to the beginning of the alphabet.
- Order 14-26: Similar to Order 1-13, but it loops through all cards Ace through King again aligned to the second half of the alpha which is also 13 letters.
- Intuitive: Once the rest of the table was filled, I could tell from early card draw simulations (which I scripted with code to run many thousands of draws) that the distribution of letters was not yet broad enough to create good results. I used AI to help by generating a list of the 14 most commonly used letters in English and then made partially logical and partially intuitive associations with the 14 blank cells (the "3rd Value" 9th row and the last column), avoiding very obvious problems like duplicating letters in the row or leaving a row with only very infrequently used letters. I made some final adjustments until it felt right.
Generating the Words
Once I had the cipher, generating the words was a fairly simple task for code. To try by hand would take a ridiculous amount of time, though it could be done. The basic idea is to get at the set of 5 letters associated with 4 card ranks in order, then generate all of the possible combinations of those letters and match those against a list of known 4-letter words. I am using a standard dictionary that seems fairly complete although it does contain some rather obscure words and variants.

The online version I linked above makes it easy to understand the meanings, value and themes of the words using a pre-formatted prompt that can be passed to an AI like ChatGPT. This is certainly not an exact methodology and it may not even be an ideal way to encode card values. However, it works, and it was both inspiring and exciting to find something that worked. Among other interesting things hidden in the cipher I will leave to the curious, the letters for 7 can form Egypt. It felt right.
Understanding the Math
If you are wondering about how likely the associations are to be repeated, we can get some sense of the scale of the possible outcomes. Anecdotally, the number of words that is matched for a 4-card set is typically somewhere between 1 and 20. The total number of letter combinations for a set is 625, or 5⁴. Those are then matched against the word list which contains 4,995 words to create a result.
Since order matters for the 4-card set, the number of combinations is 13⁴ which is 28,561. As a result, the total number of derived word combinations would be 625 times 28,561, which is 17,850,625. Clearly the scale quickly becomes completely impractical to manually generate or predict. This variation likely means there is some repetition of words or even word sets, but in practice so far I haven't seen much of that myself. Fun coincidences for my fellow number-obsessed folks: adding the digits of each of the 3 numbers here results in 13, 22, and 33.

